Just like that infamous Chinese spy balloon, some problems just keep floating around, waiting for someone to take a shot. So, let's tackle one of those today: the cons, car, and cdr functions. It's a classic.
❓ PROMPT
cons(a, b) constructs a pair, and car(pair) and cdr(pair) returns the first and last element of that pair. For example, car(cons(3, 4)) returns 3, and cdr(cons(3, 4)) returns 4.
🔍 EXPLORE
Alright, let's break this down! The cons function takes in two values, a and b, and returns a function pair that takes another function f as its argument. This inner function pair then applies f to a and b.
To get the values of a and b back, we need to pass functions to the pair function that will return the desired values.
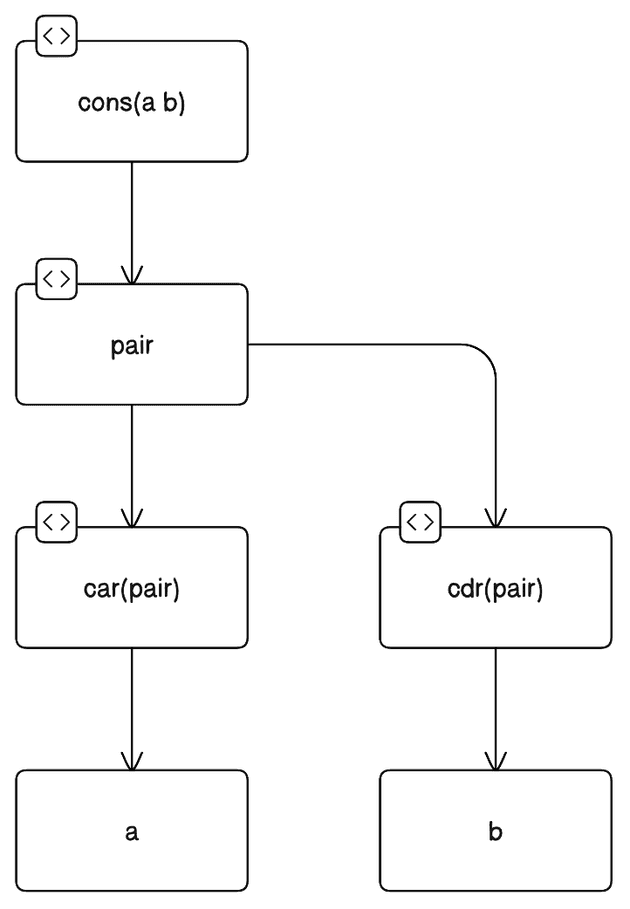
- `cons` is the main function that creates the `pair`.
- `pair` is the inner function returned by `cons` that holds the values `a` and `b`.
- `car` and `cdr` are functions that interact with `pair` to retrieve the values `a` and `b`, respectively.
Assumptions
- The function
carshould return the first element of the pair. - The function
cdrshould return the second element of the pair.
Potential Edge/Corner Cases
- What if
aorbare not simple values but complex data structures? - What if
aorbare functions themselves?
🗣️ CLARIFYING QUESTIONS
The challenge seems clear, but I'll keep in mind the potential edge cases.
💡 BRAINSTORM
To implement car and cdr:
- For
car, we can pass a function topairthat returns its first argument. - For
cdr, we can pass a function topairthat returns its second argument.
📝 PLAN
- Implement the
consfunctions. - Implement the
carfunction that takes a pair and returns the first element. - Implement the
cdrfunction that takes a pair and returns the second element.
Let's jot down some pseudocode:
function cons(a, b):
function pair(f):
return f(a, b)
return pair
function car(pair):
return pair(lambda x, y: x)
function cdr(pair):
return pair(lambda x, y: y)🛠️ IMPLEMENT
func cons<A, B>(_ a: A, _ b: B) -> (() -> (A, B)) {
return { () -> (A, B) in
return (a, b)
}
}
func car<A, B>(pair: () -> (A, B)) -> A {
let (a, _) = pair()
return a
}
func cdr<A, B>(pair: () -> (A, B)) -> B {
let (_, b) = pair()
return b
}📊 ANALYZE:
The time complexity of both car and cdr is O(1) since they directly return values without any loops or recursive calls. The space complexity is also O(1) as no additional space is used that grows with input size.
📚 Final Thoughts
In the ever-evolving world of coding, some challenges stand the test of time, not because they're unsolvable, but because they encapsulate fundamental principles. The cons, car, and cdr functions are a testament to this. They remind us that beneath the layers of complex algorithms and flashy frameworks, the basics remain crucial. Mastering foundational concepts is the key for this stuff. Sometimes, it's all about getting back to the basics. And who knows? The solution might just be simpler than you think.