Let's crush this like Beyoncé at the Grammy's last night. Some coding challenges get paraded around like they're the next big thing, only to fade into obscurity by next week. And then there are challenges like the XOR linked list. Not because they're trendy or have a flashy marketing campaign, but because they've actually got substance. It's almost as if - and bear with me here - understanding the basics is still important. Shocking, I know.
❓ PROMPT
An XOR linked list is a more memory efficient doubly linked list. Instead of each node holding next and prev fields, it holds a field named both, which is an XOR of the next node and the previous node. Implement an XOR linked list; it has an add(element) which adds the element to the end, and a get(index) which returns the node at index.
🔍 EXPLORE
Alright, let's break down this intriguing XOR linked list. At its core, it's a doubly linked list, but with a twist. Instead of two pointers for the next and previous nodes, we have one pointer that's the XOR of the two. This is a neat trick to save memory, but it does make things a tad more complex.
What is XOR?
XOR stands for "exclusive or." It's a bitwise operation that takes two bits and returns 1 if exactly one of the bits is 1, and 0 otherwise. Here's a quick truth table:
| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
The magic of XOR is that it's reversible. If you have A XOR B = C, then A XOR C = B and B XOR C = A.
Why XOR in a Linked List?
In a traditional doubly linked list, each node has two pointers: one to the previous node and one to the next node. This can be memory-intensive. The XOR linked list reduces the memory footprint by storing a single value, both, which is the XOR of the addresses of the previous and next nodes. By keeping track of the current and previous node addresses during traversal, we can compute the next node's address.
Bitwise Operations and Bit Shifting:
Bitwise operations, like XOR, operate on individual bits of numbers. In our XOR linked list, we'll be using the XOR operation to combine and extract memory addresses.
Bit shifting is the process of moving bits left or right in a binary number. It's a fundamental operation in low-level programming and can be used to multiply or divide numbers by powers of two. In our implementation, we won't be using bit shifting directly, but understanding it can help grasp the nuances of bitwise operations.
Assumptions:
- The list starts empty.
- The
bothfield of the first node (head) is just the XOR ofnulland the next node. - The
bothfield of the last node (tail) is the XOR of the previous node andnull. - We'll need to traverse the list from the start to get to any node, as we don't have direct pointers.
Discoveries:
- To traverse the list, we'll need to remember the previous node we visited. This is because the XOR operation is reversible. If we have the previous node and the both field, we can get the next node.
- To add an element to the end, we'll need to traverse the entire list.
Edge/Corner Cases:
- Adding to an empty list.
- Getting from an empty list.
- Getting an index out of bounds.
🗣️ CLARIFYING QUESTIONS
The prompt seems clear, but I do have a question: What should we return if the index is out of bounds in the get(index) method? For simplicity, I'll assume we return null in such cases.
💡 BRAINSTORM
Approach 1:
Use a traditional doubly linked list and just XOR the two pointers to get the both field. This is more of a brute force approach and doesn't take advantage of the XOR properties.
Approach 2 (The Master Plan):
- For
add(element):- If the list is empty, create a new node with
bothasnull XOR nextNode. - If not, traverse to the end and update the last node's
bothto include the new node.
- If the list is empty, create a new node with
- For
get(index):- Start from the head and traverse to the desired index using the XOR property to move forward.
This approach is efficient in terms of space as it uses the XOR property to its fullest. The time complexity for both operations is O(n) in the worst case, as we might need to traverse the entire list.
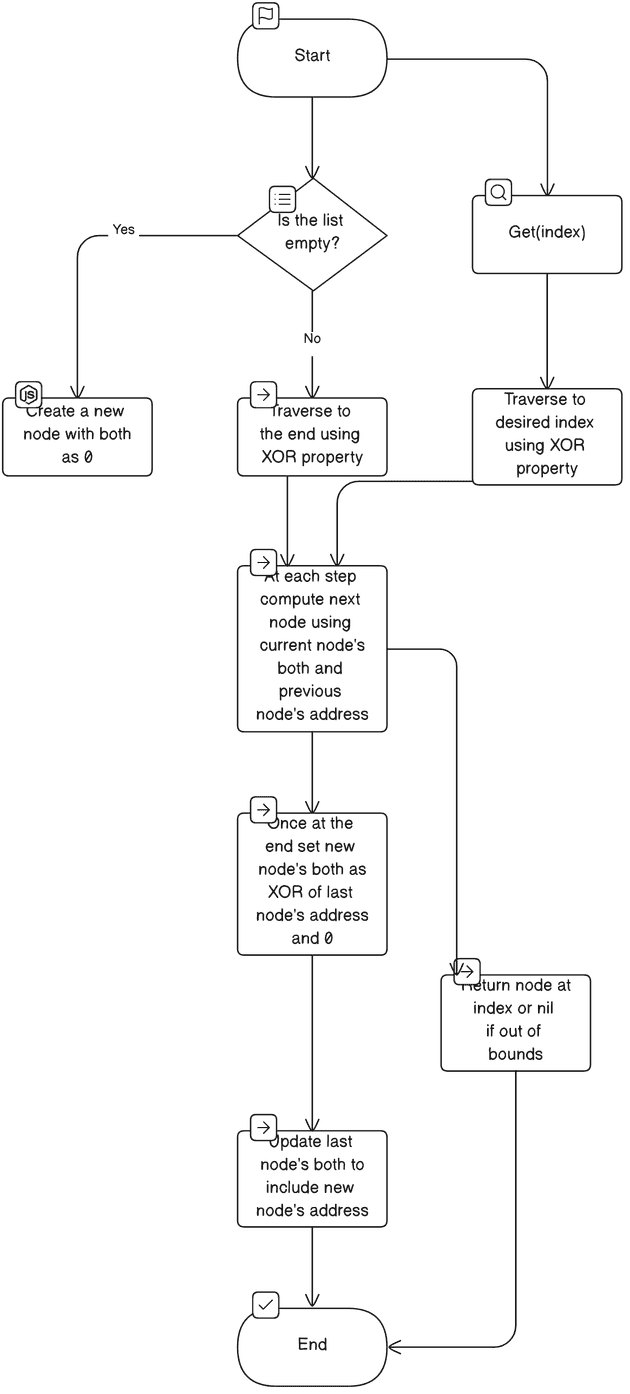
📝 PLAN
- Node Structure:
- Each node will have an
elementto store the value. - Each node will also have a
bothfield, which is the XOR of the addresses of the previous and next nodes.
- Adding an Element:
- If the list is empty, the new node's
bothwill be 0 (since there's no previous or next node). - If the list has nodes, traverse to the end. During traversal, compute the next node's address using the current node's
bothand the previous node's address. - Once at the end, set the new node's
bothto the XOR of the last node's address and 0 (since there's no next node). Update the last node'sbothto include the new node's address.
- Getting an Element by Index:
- Start at the head. Traverse the list, computing the next node's address using the current node's both and the previous node's address.
- If we reach the desired index or exceed the list's bounds, stop.
- Safety Checks:
- For the
getmethod, if the index is out of bounds, returnnull.
Let's visualize this with a diagram.
🖍️ DIAGRAM
🛠️ IMPLEMENT
class Node {
var element: Int
var both: Int
init(element: Int, both: Int) {
self.element = element
self.both = both
}
}
class XORLinkedList {
private var head: Node?
private var tail: Node?
func add(_ element: Int) {
let newNode = Node(element: element, both: 0)
if let tail = self.tail {
let prevXOR = tail.both
tail.both = prevXOR ^ (newNode as! Int)
newNode.both = (tail as! Int)
self.tail = newNode
} else {
head = newNode
tail = newNode
}
}
func get(_ index: Int) -> Node? {
var prev: Node? = nil
var current = head
for _ in 0..<index {
let next = (prev as! Int) ^ current!.both
prev = current
current = next as? Node
}
return current
}
}🧪 VERIFY
😢 The code doesn't compile.
🔄 REVIEW AND REFACTOR
Swift's emphasis on production-ready code is proving challenging for this algorithm. Here are some insights:
-
Memory Safety: Swift prioritizes memory safety. Unlike languages like C or C++, which allow direct memory manipulation, Swift enforces stricter rules to prevent unintended memory access or modification. This is evident in our challenges with using raw pointers in the XOR linked list implementation.
-
Interoperability with C: Swift is designed to be interoperable with C. This means Swift can use C libraries and vice versa. However, when using C functionalities, one must be cautious as it might bypass some of Swift's safety mechanisms.
-
Pointer Types: Swift offers several pointer types, such as UnsafePointer, UnsafeMutablePointer, and their raw counterparts. These pointers allow for direct memory access, but as the name suggests, they are "unsafe" and should be used with caution.
-
Memory Management: Swift employs Automatic Reference Counting (ARC) for memory management. This differs from manual memory management in languages like C. While ARC simplifies many tasks, it also means that developers need to be aware of reference cycles and other potential pitfalls.
-
Value vs. Reference Types: Swift has both value types (like structs) and reference types (like classes). This distinction can impact how data is stored and accessed in memory.
-
Bridging: Swift provides bridging between Swift types and their corresponding C types. This is especially useful when working with C libraries or when needing to perform operations that are more straightforward in C.
Given these insights, our approach to the XOR linked list problem in Swift should consider the following:
-
Memory Safety: We should avoid direct memory manipulation unless absolutely necessary. Instead, we can use Swift's built-in types and functionalities to achieve our goals.
-
Pointer Usage: If we must use pointers, we should ensure that we're using them correctly and safely. This includes properly initializing, deinitializing, and avoiding unintended memory access.
-
Simplicity: Rather than trying to directly translate a solution from a language like C to Swift, we should aim for a solution that aligns with Swift's paradigms and best practices.
💡 BRAINSTORM AGAIN
Given Swift's emphasis on memory safety and the challenges with raw pointers, let's consider alternative approaches:
Approach 1: Indirect Addressing: Instead of directly using memory addresses, we can use an array to store nodes. The index of each node in the array can act as its "address". The XOR operation can then be performed on these indices. This approach abstracts away direct memory manipulation and aligns better with Swift's paradigms.
Approach 2: Direct Memory Manipulation: This is the approach we initially tried, where we use raw pointers to directly manipulate memory. Given the challenges we faced and the insights from the article, this approach might not be the most suitable for Swift.
Considering the insights and Swift's strengths, Approach 1 seems more promising. It's more in line with Swift's memory safety principles and avoids the complexities of raw pointer manipulation.
🛠️ IMPLEMENT AGAIN
final class Node {
var value: Int
var both: Int
init(value: Int, both: Int) {
self.value = value
self.both = both
}
}
final class XORLinkedList {
private var nodes: [Node] = []
private var headIndex: Int? = nil
private var tailIndex: Int? = nil
func add(element: Int) {
let newNode = Node(value: element, both: tailIndex ?? -1)
nodes.append(newNode)
if let tail = tailIndex {
nodes[tail].both ^= nodes.count - 1
} else {
headIndex = 0
}
tailIndex = nodes.count - 1
}
func get(index: Int) -> Int? {
if index < 0 || index >= nodes.count {
return nil
}
var prevIndex: Int? = nil
var currentIndex: Int? = headIndex
for _ in 0..<index {
let nextIndex = (prevIndex ?? -1) ^ (currentIndex != nil ? nodes[currentIndex!].both : -1)
prevIndex = currentIndex
currentIndex = nextIndex
}
return currentIndex != nil ? nodes[currentIndex!].value : nil
}
}🧪 VERIFY
It compiles! Let's test our code:
// Testing the XOR linked list
let xorLinkedList = XORLinkedList()
// Adding elements to the list
xorLinkedList.add(element: 1)
xorLinkedList.add(element: 2)
xorLinkedList.add(element: 3)
xorLinkedList.add(element: 4)
// Getting elements by index
print(xorLinkedList.get(index: 0) ?? "nil") // Expected: 1
print(xorLinkedList.get(index: 1) ?? "nil") // Expected: 2
print(xorLinkedList.get(index: 2) ?? "nil") // Expected: 3
print(xorLinkedList.get(index: 3) ?? "nil") // Expected: 4
print(xorLinkedList.get(index: 4) ?? "nil") // Expected: nil (out of bounds)
xorLinkedList.add(element: 5)
xorLinkedList.add(element: 6)
print(xorLinkedList.get(index: 4) ?? "nil") // Expected: 5
print(xorLinkedList.get(index: 5) ?? "nil") // Expected: 6
print(xorLinkedList.get(index: 6) ?? "nil") // Expected: nil (out of bounds)🔄 REVIEW AND REFACTOR
-
Code Readability and Clarity: The code is structured with clear class definitions and method names. The use of the nodes array to simulate memory and the indirect addressing approach makes the logic more readable in Swift.
-
Swift Best Practices: The code adheres to Swift best practices. The use of optionals (Int?) ensures safe unwrapping of values. The naming conventions are consistent with Swift guidelines.
-
Potential Optimizations: The current approach uses an array to simulate memory, which might not be the most memory-efficient way in a real-world scenario. However, for the sake of this exercise and given Swift's memory management model, it's a practical approach.
-
Edge Cases: The code handles out-of-bounds indices by returning nil. This is a safe way to indicate that the requested index doesn't exist in the list.
-
Refactor Considerations: At this point, the code seems optimized for the problem at hand. However, one could consider adding more utility methods or error handling for robustness.
📊 ANALYZE
Alright, let's put on our monocles and dive deep.
Time Complexity:
add(element:): O(n) - We're essentially traversing to the end of the list to add a new element.get(index:): O(n) - In the worst case, we might need to traverse the entire list to get to the desired index.
Space Complexity:
- O(n) - The space grows linearly with the number of elements added to the list, thanks to our nodes array.
Limitations:
- Memory Simulation: Using an array to simulate memory is a neat trick, but it's not how real memory works. In a real-world scenario, we'd have to consider memory fragmentation, garbage collection, and other complexities.
- Traversal: Since we don't have direct pointers to each node, we need to traverse from the start to get to any node. This makes random access slower compared to traditional linked lists.
Potential Improvements:
- Enhanced Traversal: We could potentially speed up traversal by maintaining an index cache or using a hybrid approach with some direct pointers.
- Memory Management: In a more advanced implementation, we could consider a custom memory allocator to simulate real memory more closely.
🤔 SIMILAR QUESTIONS
- Doubly Linked List: The XOR linked list is a memory-efficient version of the doubly linked list. Implementing a traditional doubly linked list would be a good exercise to understand the differences and similarities.
- Circular Linked List: What if the list loops back to the start? How would the XOR operation work in such a scenario?
- Reverse XOR Linked List: Can you reverse the XOR linked list in O(1) time? Hint: You might not need to change the structure at all.
🌟 FINAL THOUGHTS
The XOR linked list is like that indie movie that didn't make it big at the box office but has a cult following. It's not mainstream, but it's got depth and character. It's a reminder that sometimes, looking at old problems with a new perspective can lead to innovative solutions. And while it might not be the go-to data structure for everyday use, it's a testament to the power of bitwise operations and the versatility of linked lists.
In the world of coding, where new frameworks and languages pop up every other day, it's easy to get caught up in the hype. But sometimes, it's the classics, the fundamentals, that truly stand the test of time. The XOR linked list is one such classic. It's not flashy, it's not trendy, but it's solid, reliable, and downright clever.
So, the next time you're faced with a coding challenge, remember the XOR linked list. Remember that sometimes, the best solutions come from rethinking the basics. And always, always, keep exploring, keep learning, and keep coding.
Until next time, keep your bits and bytes in check and may your code always compile on the first try (yeah, right!).