forced push

Problem 5

February 05, 2023

Just like that infamous Chinese spy balloon, some problems just keep floating around, waiting for someone to take a shot. So, let's tackle one of those today: the cons, car, and cdr functions. It's a classic.

❓ PROMPT

cons(a, b) constructs a pair, and car(pair) and cdr(pair) returns the first and last element of that pair. For example, car(cons(3, 4)) returns 3, and cdr(cons(3, 4)) returns 4.

🔍 EXPLORE

Alright, let's break this down! The cons function takes in two values, a and b, and returns a function pair that takes another function f as its argument. This inner function pair then applies f to a and b.

To get the values of a and b back, we need to pass functions to the pair function that will return the desired values.

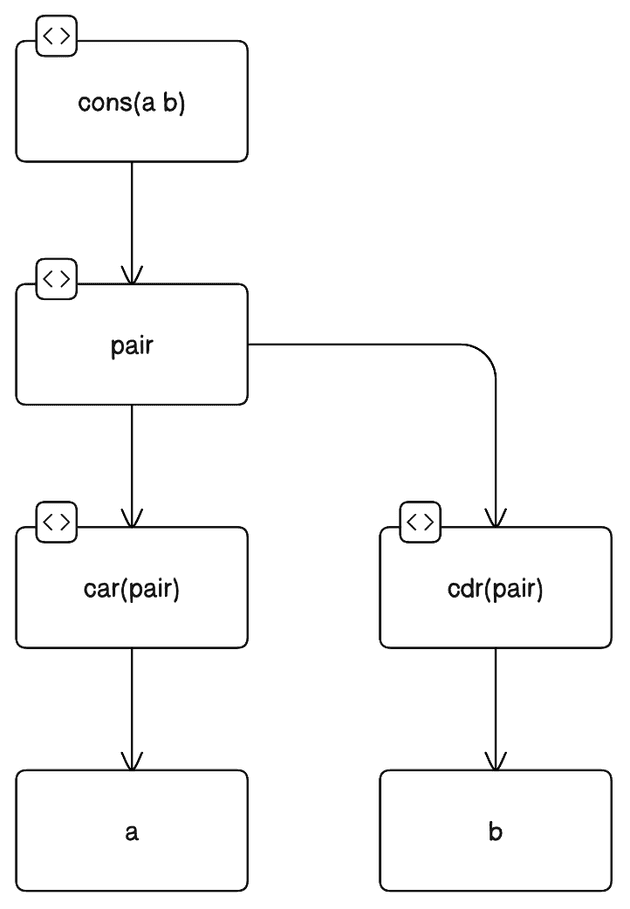
Diagram of cons, car, and cdr functions
  • `cons` is the main function that creates the `pair`.
  • `pair` is the inner function returned by `cons` that holds the values `a` and `b`.
  • `car` and `cdr` are functions that interact with `pair` to retrieve the values `a` and `b`, respectively.

Assumptions

  • The function car should return the first element of the pair.
  • The function cdr should return the second element of the pair.

Potential Edge/Corner Cases

  1. What if a or b are not simple values but complex data structures?
  2. What if a or b are functions themselves?

🗣️ CLARIFYING QUESTIONS

The challenge seems clear, but I'll keep in mind the potential edge cases.

💡 BRAINSTORM

To implement car and cdr:

  1. For car, we can pass a function to pair that returns its first argument.
  2. For cdr, we can pass a function to pair that returns its second argument.

📝 PLAN

  1. Implement the cons functions.
  2. Implement the car function that takes a pair and returns the first element.
  3. Implement the cdr function that takes a pair and returns the second element.

Let's jot down some pseudocode:

function cons(a, b):
    function pair(f):
        return f(a, b)
    return pair

function car(pair):
    return pair(lambda x, y: x)

function cdr(pair):
    return pair(lambda x, y: y)

🛠️ IMPLEMENT

func cons<A, B>(_ a: A, _ b: B) -> (() -> (A, B)) {
    return { () -> (A, B) in
        return (a, b)
    }
}

func car<A, B>(pair: () -> (A, B)) -> A {
    let (a, _) = pair()
    return a
}

func cdr<A, B>(pair: () -> (A, B)) -> B {
    let (_, b) = pair()
    return b
}

📊 ANALYZE:

The time complexity of both car and cdr is O(1) since they directly return values without any loops or recursive calls. The space complexity is also O(1) as no additional space is used that grows with input size.

📚 Final Thoughts

In the ever-evolving world of coding, some challenges stand the test of time, not because they're unsolvable, but because they encapsulate fundamental principles. The cons, car, and cdr functions are a testament to this. They remind us that beneath the layers of complex algorithms and flashy frameworks, the basics remain crucial. Mastering foundational concepts is the key for this stuff. Sometimes, it's all about getting back to the basics. And who knows? The solution might just be simpler than you think.

Logo